遗传范畴与可裂 torsion pair
遗传范畴的 torsion pair
本节的范畴要求有足够投射对象, 且 tilting 对象 $T$ 使得一切 $(T,X)$ 均是有限生成右 $\mathrm{End}(T)$-模. 一个较弱的条件是 $\mathrm{Hom}$-群有限维.
仿照三角范畴, 定义 Abel 范畴的厚子范畴为, 关于 ses 二推三封闭的全子范畴.
(遗传范畴). 称 Abel 范畴遗传, 若米田积意义下的 $\mathrm{Ext}^2(-,-)$ 函子消失.
(证明) 遗传范畴中的满单分解均可补全作推出拉回方块.
(证明). 遗传范畴中, $X^∙$ 与 $H^∙(X)$ (同调群构成的轴复形) 导出等价.
(遗传范畴的 Tilting 对象). 称 $T ∈ 𝒜$ 是 tilting 对象, 若 $T$ 生成的厚子范畴是 $𝒜$, 且 $\mathrm{Ext}^1(T,T)=0$.
可以发现, 遗传范畴中的 tilting 对象与通常意义的 tilting 模是兼容的.
- 遗传对应 $p.\dim T ≤ 1$,
- $T$ 生成厚子范畴的条件对应 $A$ 的 $𝐚𝐝𝐝(T)$-余消解维度 $≤1$,
- $\mathrm{Ext}^1(T,T) = 0$ 保持不变.
(遗传范畴的 torsion pair, 证明). 对上述遗传范畴与 tilting 对象 $T$.
- $(\ker \mathrm{Ext}^0(T,-), \ker \mathrm{Ext}^1(T,-))$ 是 torsion pair, 记作 $(𝒯, ℱ)$.
- BB 导出等价给出 $(𝒳 , 𝒴) ≃ (ℱ[1], 𝒯)$.
- 若 $B$ 遗传, 则 $(𝒯, ℱ)$ 可裂.
示意图如下:
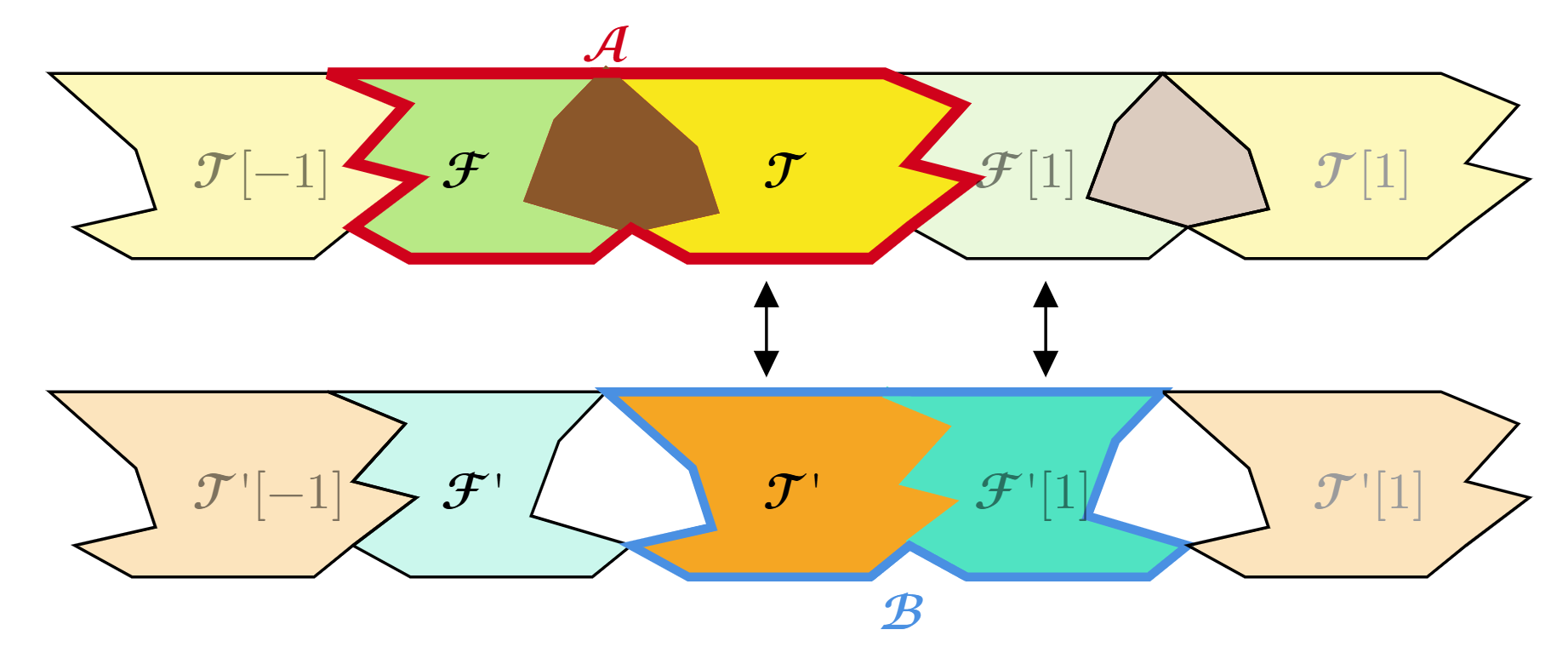
(可裂 torsion pair 的等价定义). 称 Abel 范畴 $𝒜$ 中的 torsion pair $(𝒯, ℱ)$ 可裂, 若以下等价命题成立.
- $𝒯∪ℱ$ 包含一切不可分解对象.
- $\mathrm{Ext}_𝒜^1(ℱ, 𝒯) = 0$.
- $𝒯$ 关于 $τ⁻¹$ 封闭.
- $ℱ$ 关于 $τ$ 封闭.
依次证明所有命题与 1. 等价.
-
(1 ⇒ 2). 对任意 ses $0 → T → E → F → 0$. 由假定, $E ∈ ℱ ⊕ 𝒯$. 上述 ses 的矩阵形式是
$$ 0 → T \xrightarrow {\binom a0} E_𝒯 ⊕ E_ℱ \xrightarrow{(0 \ b)} 0. $$
显然 $a$ 与 $b$ 必是同构.
-
(2 ⇒ 1). 若不然, 则存在不可分解的对象 $X ∉ (𝒯 ∪ ℱ)$. 此时存在三项非零的典范短正合列
$$ 0 → tX → X → fX → 0 $$
由 ses 可裂, 得 $X ∈ 𝒯 ⊕ ℱ$, 与假定矛盾.
- (1 ⇒ 3). 任取 $T ∈ 𝒯$, 考虑几乎可裂 ses $0 → T → ⨁ E_i → τ⁻¹ T → 0$. 由 $(T,E_i) ≠ 0$, 以及不可分解对象 $E_i ∈ 𝒯 ∪ ℱ$, 只能有 $E_i ∈ 𝒯$. 因此, $τ⁻¹ T ∈ 𝒯$.
- (3 ⇒ 2 ⇒ 1). 若 $(τ⁻¹𝒯 , ℱ) = 0$, 由 AR 公式知 $\mathrm{Ext}^1(ℱ , 𝒯 ) = 0$. 进而有 1.
- (1 ⇒ 4 ⇒ 1). 与 1 ⇒ 3 ⇒ 1 d 证明完全对偶.